Алгоритм RSA является наиболее популярным и используемым в криптографии. Использует асимметричное шифрование. На рынке информационной безопасности он уже давно, его используют в большинстве программных и не только продуктов. Здесь мы рассмотрит сам пример реализации.
АЛГОРИТМ RSA
Итак, во-первых как и в любых асимметричных шифровальщиков мы должны создать пару ключей.
- Выбираются 2 простых числа p и q. Для нашего примера возьмём p=5, а q=11
- Далее вычисляется произведение этих чисел, которое называется модулем. n=p*q. В нашем примере n=5*11=55
- На этом этапе нужно высчитать функцию Эйлера по формуле
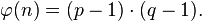Функция Эйлера определяет количество целых положительных чисел, не превосходящих n и взаимно простых с n. В нашем примере 
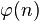=4*10=40 - Далее выбирается произвольное целое число
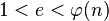. Для нашего примера я взял число 17, для стойкости алгоритма лучше брать числа содержащие небольшое количество единичных бит в двоичной записи.Таким образом у нас есть пара чисел (e,n)=(17,55), которые будут использованы для шифрования и называются открытым ключом. - Теперь самая нелюбимая часть алгоритма, это выборка числа d, вычисляется по формуле
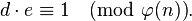из этого мы получим соотношение 
. Итак, k выбирается таким образом, чтобы в итоге d стало целым числом, k=1,2,3,4,5…..пока не найдем d, в нашем примере k=14, а значит d=33. - Пара чисел (33,55) являются закрытым ключом.
- Теперь давайте зашифруем какое-нибудь сообщение, оно шифруется по формуле
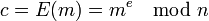, где m -шифруемый символ. Расшифруем по формуле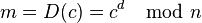 
Предположим нужно зашифровать слово xmalax, оно имеет символы в английском алфавите так (24, 13,1, 12, 1, 24)
- 24^17 mod 55=29
- 13^17 mod 55=18
- 1^17 mod 55=1
- 12^17 mod 55=12
- 1^17 mod 55=1
- 24^17 mod 55= 29
Теперь наше сообщение имеет вид (29,18,1,12,1,29)
- 29^33 mod 55=24
- 18^33 mod 55=13
- 1^33 mod 55=1
- 12^33 mod 55=12
- 1^33 mod 55=1
- 29^33 mod 55= 24
Расшифрованное сообщение полностью соответствует нашему xmalax = (24, 13,1, 12, 1, 24).
Если шифровать программно, то сам процесс займет определенное время из-за больших вычислений. Если вы пишете шифровальщик, то как минимум ваша программа должна соответствовать
- Реализация генератора простых случайных чисел.
- Эффективная и надежная реализация больших чисел(BigInteger)
- Реализация алгоритма генерации ключей, не подверженных известным атакам.
В будущем, когда квантовые процессоры войдут в нашу бытовую жизнь, RSA канет в лету. Конечно придумываются различные схемы для дополнительной защиты, но всё равно техники и мощность компьютеров с каждым годом растет и взлом это вопрос времени
